Sejj [Cjj12 421
gl的估计也在上述假设下无偏(森和斯利瓦斯塔瓦1990):
Pj j = 0, 1。gl的属性回归参数估计持有当然也WLS (gl的一个特例,V与不平等的斜对角元素)和OLS (gl的一个特例,V是对角线相等的对角元素)。OLS的情况,标准错误可以用短的显式形式(1992年蒙哥马利和派克):
2 r n / f " \ n \ 2 ^ 1/2
se ^ = MSEf 1 / n + (E t (i) /) / (E t (i) 2 - (E t (i)) / n我= 1 = 1 = 1
0.90
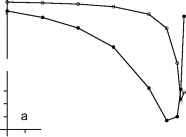
0.5 0.6 0.7 0.8 0.9 1.0自相关系数,

我- | - | - |我- 0.85 0.5 0.6 0.7 0.8 0.9 1.0自相关系数,

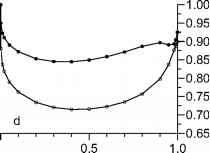
1.0 - 0.0 _等效自相关系数、等效自相关系数,
图4.2。gl和OLS线性回归估计的标准误差。gl标准错误,se ^, j = 0(拦截)和1(坡),给出了情商。(4.21)。OLS标准错误情况下当V不斜对角元素,给出(1992年蒙哥马利和派克)的平方根矩阵的对角元素(T) 1 T 'VT (T) 1。在每一个面板中,标准误差的比例是策划针对自相关系数(甚至间距)或相当于自相关系数(不均匀间距)的AR(1)模型Xnoise(我)。甚至间距,拦截;b甚至间距,斜坡;c间距不均匀,拦截;维不均匀间距,斜坡;符号,n = 100; open symbols, n = 1000. The uneven time spacing (c, d) was generated as t(i) = i2,i = 1,... , n and scaled to d = 1. Here, the coefficient of variation of the spacing, CVd, is approximately 3-1/2 « 0.58. The even time spacing has d(i) = 1.
在gl的情况下,计算标准错误和独联体通常需要一些矩阵操作(4.5节)。
一个假设可能会问当持有和使用OLS虽然V有一些非零元素分支。答案是,仍无偏见的OLS估计量(1992年蒙哥马利和派克),但有更大的比gl估计标准误差。这种效应的实际应用气候学的相关性如下(图4.2)。误差的大小减少gl取决于自相关和间距。对AR(1)自相关,甚至间距和数据大小从100年到1000年,减少标准错误(斜率、截距)小于13%;与一个典型的不均匀间距CVd的价值略高于0.5(图1.15),减少不到31%。有趣的是,减少甚至间距标准错误变得相当大的只有大型的自我(上面说,0.9)(图4.2 b)而不均匀间距是这种情况在大自相关范围(图4.2 c, d)。对不均匀间隔的气候时间序列回归估计可能因此确实受益于gl无论自相关是弱或强。raybet雷竞技最新
4.1.4.1 Prais-Winsten过程
方法被普莱斯和Winsten(1954)应用egl估计AR(1)假设下的持久性是气候时间序列分析的高相关性。raybet雷竞技最新这里,可变性和持久性的大小通常是未知的,需要估计。在这种情况下,下列程序(算法4.2)可以用来获得回归参数的CIs A0,答:这个词是表示古典由于其施工假定噪声的高斯形状。在许多实际情况下,单个更新循环应该已经提供一个令人满意的回归解决方案:从OLS和WLS开始,计算残差,更新V和执行gl。
4.1.4.2 Cochrane-Orcutt转换
另一个想法尊重AR(1)噪声的自相关过程是将变量。考虑
继续阅读:女朋友
这篇文章有用吗?